Blocs Protéiques

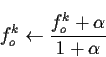
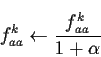
Alexandre de Brevern - Thèse de Bioinformatique Moléculaire

Prochain: Construction des familles séquentielles Au-dessus: Les familles séquentielles Précédent: Les familles séquentielles

Principe des familles séquentielles

La méthode de prédiction bayésienne implique pour chaque bloc l'utilisation d'une matrice d'occurrence qui lui est propre. Ainsi, si un bloc est composé de deux types de séquences distinctes, l'utilisation d'une matrice commune entraîne un phénomène de moyennage qui fait perdre de l'informativité à ce bloc. Aussi pour améliorer la prédiction, nous avons mis au point la méthode "des familles séquentielles". Elle consite en la génération, pour un bloc protéique x de f matrices distinctes contenant chacune une partie des fragments protéiques du BP x. Pour cela, nous avons procédé à une classification des fragments par une méthode proche des cartes topologiques de Kohonen [109].

Pour un bloc protéique x, f matrices d'occurrence sont créées. Chacune des f matrices est initialisée en mettant les fréquences des acides aminés de la matrice associée au bloc x avec une légère variation pour les individualiser. Toutes les fréquences ont été recalculées pour avoir une fréquence égale à 1 en chaque position.

Ensuite, chaque fragment protéique associé au BP x est alloué à la matrice qui lui ressemble le plus parmi les f matrices. Pour cela, la probabilité conditionnelle P_l = P(X_S/BP_k^l) est calculé pour l allant de 1 à f, avec X_S la séquence en acide aminé correspondant au fragment. Ainsi, le score maximal P_l^* = max {P_l} permet de caractériser la matrice l^* correspondant au mieux au fragment X_S. Cette matrice va être donc légèrement modifiée pour ressembler un peu plus au fragment X_S. Chaque fréquence d'acides aminés f_aa en position k est modifiée.

-

pour l'acide aminé o présenté à la position k du fragment X_S:

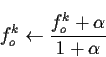
$\begin{displaymath}f_o^k \leftarrow \frac{ f_o^k + \alpha}{1 + \alpha} \end{displaymath}$

-

pour les 19 autres types d'acides aminés à la même position :

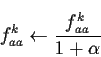
$\begin{displaymath}f_{aa}^k \leftarrow \frac{ f_{aa}^k}{1 + \alpha} \end{displaymath}$

Cette transformation permet de conserver en chaque position une somme des fréquences toujours égale à un. Le coefficient d'apprentissage $\alpha$ est égal à $\alpha_{0} /( 1 + t / N_x )$ , avec $\alpha_{0}$ le taux initial d'apprentissage pris égal à 0,05, t représentant le nombre de fragments déjà vus et N_k, le nombre total de fragments associés au bloc protéique x. Le processus est itératif, l'ensemble des fragments est donc vu totalement à chaque cycle. Au bout d'un certain nombre de cycles, les fragments se focalisent sur une seule des f matrices. 5 cycles ont été utilisés dans cette apprentissage.

$\begin{sidewaysfigure}% latex2html id marker 2168 [htbp] \centerline{\epsfxsize... ...'occurrences associ\'ees \\lq a des familles s\'equentielles.} \end{sidewaysfigure}$

Page 83