Alexandre de Brevern - Thèse de Bioinformatique Moléculaire

   
Le "nombre équivalent de blocs" (N_eq): un indice de confiance de prédiction

Après avoir prédit à partir de la séquence le (ou les) bloc protéique(s) le(s) plus probable(s) en appliquant le principe des familles séquentielles (n séquences - 1 repliement local). Nous avons décidé d'introduire un concept flou 1 séquence - n repliements qui prend en compte le fait qu'une séquence peut être associée à plusieurs types de repliements, donc plusieurs types de blocs protéiques. En observant les résultats de la prédiction, le bloc réel est souvent le plus probable, mais il est surtout fort souvent parmi les plus probables. En conséquence, j'ai essayé de définir des stratégies pour sélectionner le nombre optimal de blocs r à prendre en compte en chaque site pour avoir un taux de prédiction donné.

Dans la suite de ce chapitre, deux types de stratégies distinctes vont être utilisées. Elles se basent toutes sur deux l'entropie de Shannon et sur le fait qu'une grande homogénéité de scores R_k en un site donné veut dire que l'informativité de la séquence X_S doit être faible. La prédiction associée localement est alors peu fiable. Inversement, un score élevé pour le bloc protéique le plus probable doit être associé à un bon taux de prédiction. Dans le premier cas, il faudra choisir un nombre élevé de blocs, alors que dans le second, il en faudra moins. Pour quantifier cette incertitude, une entropie H a été calculée sur les scores R_k. Ces scores ont été dans un premier temps renormalisés en probabilités S_k :

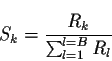
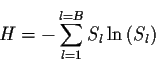
Ensuite, l'entropie H est transformée en nombre équivalent de blocs noté N_eq:

Cette quantité varie entre 1 quand un seul bloc est prédit, et, B quand les B blocs sont équiprobables. Les sites ayant un N_eq variant entre 1 et un N_eq^g (g allant de 1 à 8) ont été extraits de la base de données et le pourcentage de bonne prédiction Q_r a été ainsi calculé pour r rangs avec r variant entre 1 et 6, le bloc réel étant trouvé parmi les r rangs conservés. Les blocs sont tout d'abord classés par ordre de score décroissant.

De cette distribution, associée avec un intervalle de N_eq donné, nous déterminons le nombre rang optimal r pour assurer un taux de prédiction fixé. Cette étape a été effectuée pour tous les rangs possibles, allant de 1 à B.

Deux stratégies différentes ont ainsi été définies à partir des observations précédentes :

(i)

une approche globale qui consiste à définir un nombre variable de blocs à conserver en chaque site s pour atteindre un taux global de prédiction Q_g fixé au préalable. Dans cette optique le nombre de blocs protéiques conservés varie le long de la séquence.

(ii)

une approche locale qui tend à trouver les sites permettant pour un nombre fixé r de blocs conservés d'obtenir un taux de prédiction Q_l, lui aussi fixé au préalable. Dans cette approche, la prédiction est limitée à certaines régions des séquences protéiques.

Nous verrons donc dans une première partie, l'influence des familles séquentielles sur le N_eq, puis un exemple de prédiction sur un fragment de protéine pour voir l'évolution du N_eq, puis enfin successivement les deux stratégies.