Blocs Protéiques

Alexandre de Brevern - Thèse de Bioinformatique Moléculaire

Prochain: Apprentissage tenant compte des Au-dessus: L'apprentissage Précédent: Initialisation

Apprentissage non supervisé

A chaque cycle, les fragments sont tirés aléatoirement. La figure 3.2 récapitule l'ensemble des deux étapes du processus d'apprentissage, la figure 3.3 pour la première et la figure 3.4 pour la seconde.

**Figure 3.3:** Première étape d'apprentissage. (1) Un fragment est choisi aléatoirement dans la base de données protéique. (2). Les B distances sont calculées avec les B blocs existants. (3). Le bloc le plus proche du fragment tiré aléatoirement est modifé légèrement pour lui ressembler. (4). Le processus recommence au (1).
$\begin{figure} \centerline{\epsfxsize=17cm {\epsfbox{Images/Chapitre_3_PBs/apprentissage_01.eps}}} \end{figure}$

Dans un premier temps, l'apprentissage ne tient pas compte des transitions. (1) Un fragment est choisi aléatoirement dans la base de données d'apprentissage. (2) Son vecteur d'observation V(m) est comparé à chacun des blocs protéiques PB_k à l'aide du critère du RMSda. B comparaisons sont donc calculées. (3) Le RMSda minimal correspond ainsi au bloc le plus proche structuralement du fragment. (4) Le vecteur W(k) du bloc le plus proche est très faiblement modifié pour ressembler à celui présenté au réseau V(m):

$\begin{displaymath}\textbf{W}(k) \leftarrow \textbf{W}(k) + (\textbf{V}(m) - \textbf{W}(k)).\nu(c)\end{displaymath}$

avec $\nu(c)$ le coefficient d'apprentissage. Le symbole $\leftarrow$ veut dire "la valeur de gauche est remplacée par celle calculée à droite". Ce coefficient, initialement pris faible, i.e. $\nu_0=$ 0.02, décroit pendant l'apprentissage. $\nu(c)$ se modifie avec le nombre c de vecteurs d'observations déjà vus :

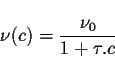
$\begin{displaymath}\nu(c) = \frac{\nu_0}{1 + \tau.c}\end{displaymath}$

avec $\tau$ fixé arbitrairement à 1/N, N représentant le nombre de vecteurs d'observations présents dans la base de donnée d'apprentissage. Dans notre cas, N = 56 442. Ainsi, $\nu(c)$ est divisé par deux après le premier passage complet de la base.

L'apprentissage est itératif, un certain nombre de cycles C (= 15) est nécessaire pour définir des vecteurs optimaux W associés aux blocs. Chaque fragment n'est utilisé qu'une seule fois par cycle.

Page 48