Alexandre de Brevern - Thèse de Bioinformatique Moléculaire

Prochain: Résultats Au-dessus: Prédiction bayésienne simple Précédent: Prédiction bayésienne simple

   
Méthodes

Pour chaque site s d'une protéine, qui comprend aussi bien la position centrale que l'ensemble de la fenêtre de la séquence [-w;+w] autour de cette position centrale, nous avons calculé pour une séquence d'acides aminés XS, la probabilité d'observer cette séquence dans un bloc donné PBk, notée P(PBk/XS).

De cette probabilité conditionnelle préalablement définie, il est possible de calculer la probabilité d'avoir ce bloc connaissant la séquence, en utilisant le théorème de Bayes. Il accomplit, en effet, l'inversion de la séquence XS et de la structure PBk:


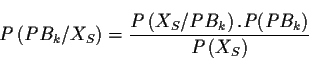
\begin{displaymath}P\left({PB_k / X_S}\right)=\frac{P\left({X_S}/{PB_k}\right).P(PB_k)}{P\left({X_S}\right)}\end{displaymath}

avec P(PBk), la probabilité d'observer PBk dans la base de données et P(XS), la probabilité d'observer la séquence d'acides aminés XS sans aucune information sur la structure. Cette dernière est égale au produit des fréquences des acides aminés dans la base de données. Une approche assez similaire a été utilisée par Thompson et Goldstein [193] pour la prédiction des structures secondaires.

Le terme P(XS/PBk) est la probabilité conditionnelle d'observer une séquence donnée XS (a-w,...,a+w) pour un bloc PBk. Il est calculé comme le produit des probabilités pour chaque acide aminé en position j dans la séquence dans le bloc (cf. figure 4.2). Ce qui amène à l'équation:


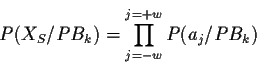
\begin{displaymath}P(X_S/PB_k)=\prod_{j=-w}^{j=+w} P(a_{j} / PB_k)\end{displaymath}

Pour définir le bloc optimal PB* pour une série d'acides aminés XS en un site s d'une protéine, nous utilisons le ratio Rk (ou son logarithme) défini par:


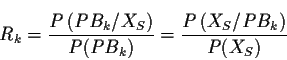
\begin{displaymath}R_k = \frac{P\left({PB_k}/{X_S}\right)}{P(PB_k)}=\frac{P\left({X_S}/{PB_k}\right)}{P(X_S)} \end{displaymath}

Du théorème de Bayes, Rk est défini par le ratio P $\left({X_S}/{PB_k}\right)$/P(XS) qui est calculé à partir des matrices d'occurrences. Grâce à ce ratio, la probabilité d'observer un bloc donné PBk sachant la séquence XS est comparé à la probabilité d'observer PBk sans avoir d'information sur la séquence. Ainsi, quand ln(Rk) est positif, la connaissance de la séquence XS est favorisée par les occurrences de PBk, et inversement quand il est négatif.

La règle pour définir le bloc optimal PB* pour la séquence XS revient à sélectionner, parmi les B blocs, le bloc PB pour lequel ce ratio Rk est maximum. Par conséquence, une liste des B blocs protéiques est définie selon leurs valeurs décroissantes de Rk, le bloc optimal étant le premier. Ainsi, nous pouvons calculer le pourcentage de bonne prédiction Q(1) au premier rang et and Q(r) quand le bloc réel est parmi les r premières solutions.


 \begin{sidewaysfigure}% latex2html id marker 2084 [htbp] \centerline{\epsfxsize... ..._aa1}), les 16 scores sont classés par ordre décroissant.} \end{sidewaysfigure}


  
Figure 4.2: Principe du calcul du score. En chaque position de la séquence, le produit des fréquences normalisées est effectué avec chaque matrice d'occurrence normalisée pour chaque BP.
\begin{figure} \centerline{\epsfxsize=10cm \rotatebox{0}{\epsfbox{Images/Chapitre_3_PBs/annexe5.ps}}} \end{figure}


Page 78

(c) 2001- Alexandre de Brevern