Alexandre de Brevern - Thèse de Bioinformatique Moléculaire

   
Par une méthode d'aggrégation en deux étapes (Unger et al., 1989, 1993)

L'objectif de ce travail est d'obtenir un grand nombre de prototypes pour pouvoir ensuite reconstruire l'ensemble des structures protéiques avec ces blocs (1989,[198] et 1993,[200]). Pour leur base de données, Unger et collaborateurs ont conservé sur les 354 chaînes présentes (PDB de janvier 1987), 82 ayant un facteur R dit "correct" et une résolution de moins de 2.8 Å, soit 12 973 résidus.

Leur méthode consiste à calculer l'écart quadratique moyen ou RMSd (root mean square deviation) entre deux structures s et t, en ne conservant que les carbones du squelette dans cette comparaison:

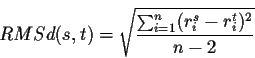
Un exemple intéressant des problèmes liés au calcul du RMSd est donné. Le RMSd minimal entre deux structures n'est pas obligatoirement une information adéquate. Ainsi la figure 2.3.2.1 montre 3 fragments protéiques. Le RMSd entre (a) et (b) est plus grand que celui entre (b) et (c), alors que le type de repliement de (a) est plus proche de celui de (b).

  

Figure: 3 fragments protéiques d'une longueur de 7 C (Figure 1. p.357 [198]).

Après un calcul préliminaire effectué sur 4 protéines (426 résidus au total), Unger et collaborateurs ont décidé de prendre comme prototypes des hexamères (i.e., des fragments de longueur 6). Ils considérent cette longueur comme la plus petite correcte pour bien différencier les fragments protéiques entre eux. L'ensemble des RMSd entre les hexamères des 4 protéines en question (soit 82 215 couples) est calculé et ensuite réuni par une méthode dite "d'annexion".

Cette procédure se passe en trois étapes:

1-

Un hexamère est tiré au hasard dans la base de données. Tous les hexamères étant à moins de 1 Å de RMSd de cet hexamère lui sont attribués. Ensuite tous les hexamères du groupe sont utilisés pour leur associer les hexamères étant à moins de 1 Å. La procédure s'arrête quand plus aucun hexamère ne peut être attribué au groupe. Un hexamère n'appartenant à aucun groupe est alors tiré au sort et le processus recommence jusqu`à l'attribution de tous les hexamères à un groupe.

2-

L'inconvénient de la première étape est de créer des groupes importants dont certains ont plus d'1 Å de RMSd. Aussi, Unger et collaborateurs redivisent les groupes et font plusieurs tentatives pour n'obtenir que des sous-groupes dont tous les hexamères sont à moins de 1 Å de RMSd les uns des autres.

3-

Le centre de chaque groupe est conservé comme bloc structural type du groupe (bloc le plus proche du barycentre calculé).

La méthode d'annexion est moins conventionnelle que la méthode des nuées dynamiques. La plus grande crainte des auteurs est de n'obtenir que fort peu de groupes dans la première étape. Elle donne 55 groupes, ce nombre étant directement lié au choix de leur valeur limite de 1 Å , qui est assez faible pour des fragments de cette taille. La seconde étape est plus criticable. En effet, rien ne laisse supposer qu'un groupe X doit être subdivisé en sous-groupe X₁ et X₂. Il est logique de penser que des éléments de X après division puissent être alors plus proches d'un autre groupe Y plutôt que X₁ ou X₂. Après la seconde étape, 103 blocs structuraux sont obtenus. Sur la base de données complète :

a-

76% des fragments sont proches d'un des blocs structuraux avec un RMSd de moins d'1 Å.

b-

92% avec moins de 1,25 Å.

c-

65% ne sont proches que d'un bloc (à moins d'1 Å).

d-

5% sont proches de plus de 2 blocs (à moins d'1 Å).

e-

En ne conservant que des fragments ayant moins de 1 Å de différence avec la réalité, 99% de leur base de données est couverte.

Utilisant 4 autres protéines, la méthode donne à 144 blocs protéiques finaux. En combinant les 8 protéines, elle atteind à 170 blocs structuraux. Les plus fréquents sont retrouvés dans les deux expériences, mais le reste est trés fluctuant. Les structures connues répétitives et leurs liens caractéristiques sont retrouvés.

Une méthode de reconstruction sur des protéines de longueur 60, ou alors sur les 60 premiers acides aminés (extrémité N-terminale), est effectuée en ajoutant à chaque fois "au mieux" un nouveau carbone correspondant au nouveau bloc protéique. La procédure consiste à superposer en une position X les 5 premiers atomes du bloc structural x avec les 5 derniers de la chaîne reconstruite. La reconstruction est correcte dans plus de 64% des cas. Seuls des changements rapides dans le repliement posent un réel problème.

En conclusion, la méthode développée par Unger et collaborateurs est intéressante car elle est basée sur une méthodologie pertinente pour regrouper des fragments protéiques, et surtout, les blocs ont servi lors d'une méthode de reconstruction 3D avec de bons résultats. Toutefois, deux points posent problémes :

(a)

Le choix de 4 protéines seulement au départ est trop faible et ne peut rendre compte de la diversité des repliements protéiques, comme le nouvel échantillonnage le montre fort bien. Un choix de 25 protéines soit 1/3 de la base de données aurait été plus judicieux. Pour éviter un temps de calcul élevé, un traitement rapide pour éliminer du regroupement des fragments vraiment trop proches, comme des coeurs d'hélices ou de feuillets, aurait été possible.

(b)

La méthode de réallocation est fortement discutable, la taille des groupes devenant rapidement très faible. Par exemple, le seizième groupe le plus important de la base de données représente 1.0%. Sur la base de données de départ de 4 protéines, il ne représente donc que 4 fragments.

L'équipe d'Unger utilisera ces blocs, comme exemple, pour une autre méthode de reconstruction, basée sur les angles dièdres [199]. Ils montrent que la plupart des hexamères trouvés sont créables par une procédure aléatoire dans les zones de Ramachandran classiques.

Enfin en 1993, Unger et Sussman réutilisent les blocs obtenus quatre ans auparavant [200], mais n'en conservent que 81, ceux-ci étant observés plus de 35 fois dans leur base de données, soit une fréquence minimale de 0,3 %. Détail troublant, les chiffres donnés sont les même que ceux obtenus pour les 103 blocs. Les hexamères obtenus se retrouvent dans les zones préférentielles du diagramme de Ramachadran, mais beaucoup sont significatifs car une procédure purement aléatoire crée beaucoup de fragments peu ou non observés dans la base de données. Ainsi, les auteurs espèrent déceler un début d'architecture des protéines avec leurs hexamères. Pour explorer un cas plus localisé, tous les blocs définis en 'brin étendu' ('E' ou feuillet dans DSSP [100]) sont extraits de la base de données. Ces différents blocs ont une répartition différente en acides aminés. Toutefois, les chiffres donnés sont en pourcentage et on ne peut juger de la valeur statistique des variations observées.

  

Figure: Représentation 3D des 82 blocs structuraux (BB) (Figure 1. p.463 [200]).