Alexandre de Brevern - Thèse de Bioinformatique Moléculaire

Pour une librairie de sous-structures (Prestrelski et al., 1992)

Prestrelski et collaborateurs ont créé une librairie de blocs, sans a priori sur le type de structures secondaires. Ils désirent les utiliser pour trouver des homologies structurales, d'une manière similaire à celle de Jones et Thirup [98], mais en concevant une librairie fixe de prototypes et non spcifiquement conçue pour une protéine unique (1992, [146]).

La base de données utilisée est composée de 14 protéines ne possédant pas d'homologie structurale, résolues à moins de 2,5 Å et représentant 2 437 résidus.

La méthode consiste en la génération d'un petit nombres de blocs différents structuralement. Le critère de similarité choisi est moins classique que dans le précédent travail. Il s'agit d'une fonction liant un critère de distance dite distance linéaire et un critère angulaire, l'angle qui décrit 4 C successifs du squelette polypeptidique. La figure 2.11 montre ces deux critères.

  

Figure 2.11: Représentation schématique de la distance linéaire et de l'angle [146].

La distance linéaire (DL) est la somme des distances C-C [122]:

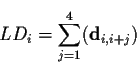
avec d_i,i+j la distance entre le C et le C . Ce critère permet de différencier les structures répétitives. Elle a été utilisée pour observer des insertions-délétions dans des structures cristallographiques. Toutefois, elle ne permet pas de différencier une hélice gauche d'une hélice droite par exemple [122]. Pour contrecarrer ce type de problème, ils ont donc adjoint l'angle . Pour différencier deux fragments protéiques s et t, une fonction de coût C_s,t dépendant de deux paramètres C₁ et C₂ a été définie:

La valeur maximale de la différence des angles est limitée à 85^o. Pour travailler sur des fragments de taille supérieure à 5, ils ont utilisé une fenêtre glissante définie par Max= (L_f - 4 ) maxdif , avec L_f la taille du fragment considéré, maxdif la valeur maximale de la fonction de coût pour les fragments considérés. La valeur 0,75 sert à comparer des fragments de taille 8 utilisés dans l'étude et ceux de taille 5.

Quand les valeurs des distances linéaires sont proches, l'angle est très différent. L'utilisation conjugée des deux critères semble donc discriminante.

Avec cette approche, la première étape à réaliser est la calibration des deux coefficients C₁ et C₂. Pour les ajuster, ils ont testé un ensemble de valeurs de C₁ allant entre 0,1 et 1,0 et de C₂ entre 1,0 et 2,2. Pour déterminer la qualité discriminante des coefficients, ils ont testé une dizaine de prototypes d'hélices, de feuillets et de structures périodiques en calculant leurs distances linéaires, leurs angles et les valeurs de Max associées aux coefficients testés. Ensuite, ils ont choisi comme notion d'équivalence le fait que deux structures ont un RMSd inférieur à 1 Å. Les résultats ont particulièrement pris en compte la distinction entre les hélices et le reste des exemples. C₁=0,9 et C₂=2,0 ont ainsi été choisis et appliqués comme critère de coût à l'ensemble des fragments issus de la base de données.

La méthode utilisée de groupements n'est pas décrite en détail, mais aux vues des résultats donnés qui récapitulent les 30 blocs les plus fréquents, une simple recherche des coûts minimaux aurait pu suffir. Ils obtiennent au final 113 blocs distincts. Pour donner un ordre de grandeur, le deuxième bloc le plus fréquent ne représente que 17 fragments.

En conclusion, la méthodologie utilisée est peu conventionnelle. Les seuls points ambigus concernent la recherche des coefficients C₁ et C₂et la signification exacte du coût pour les fragments de longueur 8 usités. Si la formule donnée est bien celle utilisée, le seul critère important est maxdif qui représentent en fait pour chacuns des fragments, s et t. Ceci convient parfaitement pour "écarter" les fragments. On ne travaille que sur les différences maximales. Toutefois, il est possible que cette fonction génère un nombre de blocs distincts trop important. Avoir plus de 72% des blocs vus moins de 10 fois parait un peu élevé. Unger et collaborateurs ont des chiffres fort différents. Un autre facteur a pu jouer: le choix des protéines de la base de données qui sont sans homologie structurale. Au final, seules les hélices réapparaissent fortement; les feuillets sont peu présents. Cela peut être dû à leur caractéristique structurale plus lâche. Par ailleurs, les auteurs désirent faire plutôt une classification par classe de protéines. L'adjonction de 6 nouvelles protéines fait passer leur taux de recouvrement par les 30 prototypes les plus courants de 67% à 77%.

Cette méthode a été mise au point pour aider lors de travaux de spectroscopie à infra-rouge. La librairie générée leur a permis de constater des corrélations impossibles avec une autre méthode et donc de proposer une architecture de sérine-protéase compatible avec les structures connues [147].