Alexandre de Brevern - Thèse de Bioinformatique Moléculaire

   
Par une Carte-auto organisée de Kohonen (Schuchhardt et al., 1996)

L'objectif des travaux de Schuchhardt et collaborateurs est d'obtenir un grand nombre de prototypes pour approximer la structure tridimensionnelle d'une protéine dans un but de classification et d'analyse sans tenter de reconstruire cette structure (1996, [175]).

La base de données est composée de 136 protéines ayant moins de 30% de similitude de séquence [84,83], ce qui représente un total de 24 239 résidus.

La méthode consiste à caractériser les protéines en utilisant des fragments d'une longueur de 9 résidus décrits par les angles et . Les protéines sont découpées en fragments de 9 résidus donnant chacun un vecteur d'observation de longueur 16 (le premier et le dernier n'étant pas pris en compte). L'ensemble comporte donc 23 151 exemples. Schuchhardt et collaborateurs ont utilisé une méthode non supervisée d'apprentissage, les cartes de Kohonen (cf. Annexe 1 pour plus de détail). Cette méthode consiste à créer N M neurones (représentés par une matrice), chaque neurone étant une observation moyenne, ici un vecteur d'angles dièdres, à rechercher pour chaque observation de la base de données le neurone le plus proche de cette observation et lui faire apprendre cette observation. Le principe est décrit en détail dans l'annexe I. Son intérêt principal est un aspect visuel particulièrement utile pour l'analyse. La méthode des cartes de Kohonen ne diffère des nuées dynamiques ou des k-moyennes (ou k-means) [79] que par l'existence d'un processus de diffusion qui permet de réunir dans un environnement proche des neurones ayant des points communs.

Pour évaluer les différences entre les observations, une mesure de dissemblance, le RMSda ou root mean square deviation on angular values est utilisée. Cette distance sur les angles a déjà servi dans une méthode de recherche d'homologie structurale [102]. Il s'agit d'une distance euclidienne entre deux vecteurs d'observations s et t:

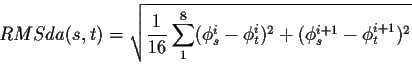
La figure 2.12 montre la carte de Kohonen obtenue pour une taille de 10 10, soit 100 neurones. Cette carte est "plane", ce qui veut dire qu'elle possède des bords, le neurone (9/9) n'est voisin que des neurones (8/8), (8/9) et (9/8), alors qu'au milieu de la carte, un neurone est entouré de 8 voisins.

  

Figure 2.12: Carte auto-organisée de Kohonen obtenue pour 100 neurones (Figure 4a. p.836 [175]). Chaque neurone est décrit par la suite des 16 angles dièdres moyens.

Les feuillets et les hélices se retrouvent dans des neurones distincts. Les hélices sont fortements localisées en haut et à gauche de la carte, les feuillets plus sur la droite. La validation structurale est effectuée exclusivement sur le critère du RMSda et les résultats semblent satisfaisants. Des motifs dits de "cassure" classique avec une forte proportion de Glycine sont trouvés. Quelques exemples de suivi de trajectoires de protéines sur la carte sont montrés.

La méthode est particulièrement appropriée à la recherche et à l'analyse de données biologiques, comme le montre le travail de Hanke et Reich sur la reconnaissance de motifs propres à des familles protéiques [77,78]. L'utilisation des angles dièdres avec le RMSda est beaucoup plus souple que le classique RMSd. Du fait de sa rapidité, un travail plus important sur les différents paramètres de l'apprentissage est possible. Les résultats sont convaincants. Toutefois, ayant refait leurs expériences, deux points me paraissent importants :

1-

L'utilisation d'un réseau plan est peu approprié. Un réseau fermé, où les neurones ont tous 8 voisins (i.e, le neurone (9/9) est voisin des neurones (8/8), (8/9), (9/8) et (0/0), (0/8), (0/9), (9/0) et (8/0)), permet une meilleure diffusion sans effet de bord. Et, en fin d'apprentissage, les hélices et les feuillets sont bien mieux séparés. Les motifs caractéristiques sont aussi plus accentués.

2-

Une longueur de neuf résidus est un peu élevée. La recalcul des angles dièdres réels à partir d'une longueur est peu évidente. Cette méthode est donc peu utilisable en particulier pour reconstruire une protéine. De plus, la précision obtenue est parfois trés médiocre pour certains neurones, d'ailleurs aucune notion de variabilité n'est donnée dans le texte. Certains angles ont une variabilité proche de 180^o. Avec une carte plus petite, on conserve un approximation comparable, et une longueur plus faible, elle est plus intéressante, en fait.