Blocs Protéiques

Figure 3.11: Calcul des angles $\phi$ (respectivement (a) et (c)) et $\psi$ (respectivement (b) et (d))) à partir des blocs protéiques, avec l'usage d'une moyenne des 4 PBs présents (respectivement (a) et (b)), et, avec l'utilisation d'une librairie (respectivement (c) et (d)).

$\rotatebox{270}{\includegraphics[width=8cm]{Images/Chapitre_3_PBs/approx_phi.ps}}$	$\rotatebox{270}{\includegraphics[width=8cm]{Images/Chapitre_3_PBs/approx_psi.ps}}$
$\rotatebox{270}{\includegraphics[width=8cm]{Images/Chapitre_3_PBs/approx_phi-library.ps}}$	$\rotatebox{270}{\includegraphics[width=8cm]{Images/Chapitre_3_PBs/approx_psi-library.ps}}$

Ayant recodé les protéines à l'aide des bloc protéiques, il faut pouvoir ensuite approximer la structure réelle. Pour cela, une première approche simple a été mise au point. Les fragments sont chevauchants donc dans une succession de blocs tuvw, tous les PBs t, u,v, et w approximent les angles $\phi_{u}$ et $\psi_{t}$ . Ainsi, chaque site, à l'exception des résidus aux extrémités C- et N-terminales, est recodé par 4 blocs protéiques. Une moyenne entre leurs angles, pour le même site, permet un recodage simple. Il faut cependant faire attention aux effets de rotation des angles.

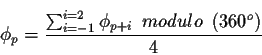
$\begin{displaymath}\phi_{p} = \frac{\sum_{i=-1}^{i=2} \phi_{p+i}\hspace{0.2cm} modulo\hspace{0.2cm}(360^{o})}{4} \end{displaymath}$

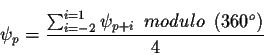
$\begin{displaymath}\psi_{p} = \frac{\sum_{i=-2}^{i=1} \psi_{p+i}\hspace{0.2cm} modulo\hspace{0.2cm}(360^{o})}{4} \end{displaymath}$

Ceci mène à une bonne approximation avec plus de 50% des angles approximés à moins de 21^o et seulement 3 % de mauvaises approximations avec plus de 90^o d'écart avec la réalité.

Pour améliorer ce recalcul des angles à partir du codage en terme de blocs protéiques, j'ai pris en compte le fait que les successions de blocs ne sont pas aléatoires (cf paragraphes 3.3.3 et 5.2). Seul un certain nombre de transitions est vu. Avec une nouvelle base de données de 553 protéines non redondantes [84,83] et ayant moins de 25% d'identité de séquences (fournie par R. Gautier), j'ai constitué pour chaque succession de 4 blocs indicés par t, u, v, w une librairie avec les angles $\phi_{u}$ et $\psi_{t}$ moyens qui leurs sont associés. Chaque fois que la succession est vue, au lieu de réutiliser la métrique moyenne, les angles moyens $\phi_{u}$ et $\psi_{t}$ associés à cette succession sont pris. Si la succession n'a jamais été vue, l'approximation se fait en réutilisant la métrique précédente. La figure 3.11 récapitule les deux approches. On peut ainsi observer que: (1) d'une manière générale les angles $\psi$ sont les moins bien approximés et ceci avec les deux méthodes et (2) le nombre d'angles mal approximés chute fortement avec l'utilisation d'une librairie. Ainsi, il y a 4 fois moins d'angles à plus de 90^o avec cette seconde méthode et 50% des angles sont approximés à moins de 10^o.

Après avoir observé dans les derniers paragraphes la stabilité structurale de la série de 16 blocs protéiques, nous allons analyser dans les paragraphes suivants les blocs sur un plan structural en observant tout d'abord les transitions qui existent entre les blocs protéiques, puis ensuite la répartition des structures secondaires associées aux blocs et enfin pour mieux comprendre par la suite la prédiction locale, les différentes répartitions des acides aminés dans les blocs protéiques.

Reproduction de la structure : amélioration par l'utilisation d'une librairie