Blocs Protéiques

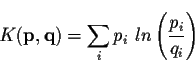
Alexandre de Brevern - Thèse de Bioinformatique Moléculaire

Prochain: Z-scores Au-dessus: Analyse des matrices d'occurrences Précédent: Analyse des matrices d'occurrences

La mesure de divergence asymétrique de Kullback-Leibler (KLd)

Pour aborder le premier point, l'entropie relative ou mesure de divergence asymétrique de Kullback-Leibler (KLd, [112]) est particulièrement utile :

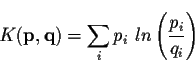
$\begin{displaymath}K(\textbf{p},\textbf{q})=\sum_i p_i \mbox{ } ln \left(\frac{p_i}{q_i}\right)\end{displaymath}$

Ce terme K quantifie la différence existante entre la distribution des acides aminés dans le bloc p $:\{p_i\}_{i=1,...,20}$ et celle attendue au vue de l'occurrence du bloc dans la base de données si tout était aléatoire. Le terme K_k(p_j,q) a été calculé en chaque position j pour observer la différence existant entre la distribution observée en acides aminés p_j et la distribution de référence de la base de donnée q ajustée pour PB_k.

Cette mesure de divergence, notée KLd, permet de détecter des positions "informatives" en observant les positions j dans l'intervalle [-w;+w].

L'entropie relative K(p,q) est une valeur toujours supérieure ou égale à zéro. Elle suit, multipliée par 2N (N étant le nombre d'observations dans la base de données), une loi classique du $\chi^2$ à 19 degrés de liberté (ou ddl, car défini sur les 20 types d'acides aminés). La valeur seuil a été choisie pour un risque $\alpha$ de premier ordre de 10^-5. Toute valeur supérieure à cette valeur seuil est donc fortement significative.

Prochain: Z-scores Au-dessus: Analyse des matrices d'occurrences Précédent: Analyse des matrices d'occurrences

Page 64